Geometric Progression, Series & Sums

Introduction

A geometric sequence is a sequence such that any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r. The common ratio (r) is obtained by dividing any term by the preceding term, i.e.,

where	r	common ratio
	a1	first term
	a2	second term
	a3	third term
	an-1	the term before the n th term
	an	the n th term

The geometric sequence is sometimes called the geometric progression or GP, for short.

For example, the sequence 1, 3, 9, 27, 81 is a geometric sequence. Note that after the first term, the next term is obtained by multiplying the preceding element by 3.

The geometric sequence has its sequence formation:

To find the nth term of a geometric sequence we use the formula:

where	r	common ratio
	a1	first term
	an-1	the term before the n th term
	n	number of terms

Sum of Terms in a Geometric Progression

Finding the sum of terms in a geometric progression is easily obtained by applying the formulas:

nth partial sum of a geometric sequence

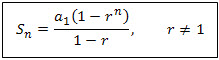
sum to infinity

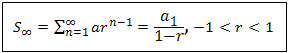
where	Sn	sum of GP with n terms
	S∞	sum of GP with infinitely many terms
	a1	the first term
	r	common ratio
	n	number of terms

Examples of Common Problems to Solve

Write down a specific term in a Geometric Progression

Question

Write down the 8th term in the Geometric Progression 1, 3, 9, ...

Answer

Finding the number of terms in a Geometric Progression

Question

Find the number of terms in the geometric progression 6, 12, 24, ..., 1536

Answer

Finding the sum of a Geometric Series

Question

Find the sum of each of the geometric series

Answer

Finding the sum of a Geometric Series to Infinity

Question

Answer

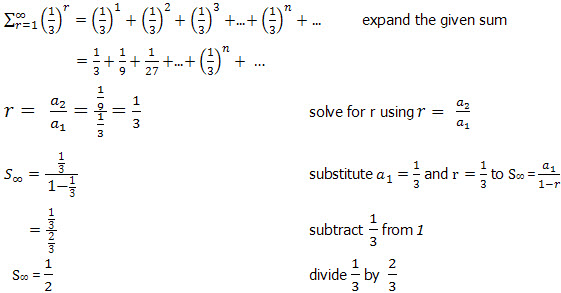
Converting a Recurring Decimal to a Fraction

Decimals that occurs in repetition infinitely or are repeated in period are called recurring decimals.

For example, 0.22222222... is a recurring decimal because the number 2 is repeated infinitely.

The recurring decimal 0.22222222... can be written as .

Another example is 0.234523452345... is a recurring decimal because the number 2345 is repeated periodically.

Thus, it can be written as or it can also be expressed in fractions.

Question

Express as a fraction in their lowest terms.

Answer

Go to the next page to start putting what you have learnt into practice.