Indices & the Law of Indices

Introduction

Indices are a useful way of more simply expressing large numbers. They also present us with many useful properties for manipulating them using what are called the Law of Indices.

What are Indices?

The expression 2⁵ is defined as follows:

We call "2" the base and "5" the index.

Law of Indices

To manipulate expressions, we can consider using the Law of Indices. These laws only apply to expressions with the same base, for example, 3⁴ and 3² can be manipulated using the Law of Indices, but we cannot use the Law of Indices to manipulate the expressions 3⁵ and 5⁷ as their base differs (their bases are 3 and 5, respectively).

Six rules of the Law of Indices

Rule 1:

Any number, except 0, whose index is 0 is always equal to 1, regardless of the value of the base.

An Example:

Simplify 2⁰:

Rule 2:

An Example:

Simplify 2^-2:

Rule 3:

To multiply expressions with the same base, copy the base and add the indices.

An Example:

Simplify : (note: 5 = 5¹)

Rule 4:

To divide expressions with the same base, copy the base and subtract the indices.

An Example:

Simplify

:

Rule 5:

To raise an expression to the nth index, copy the base and multiply the indices.

An Example:

Simplify (y²)⁶:

Rule 6:

An Example:

Simplify 125^2/3:

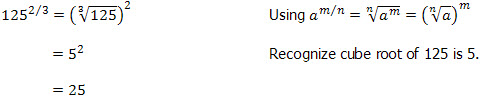
You have now learnt the important rules of the Law of Indices and are ready to try out some examples!

Go to the next page for the first of many questions and fully worked out solutions for you to practice.