Binomial Theorem and Pascal's Triangle

Introduction

Consider the 3^rd power of

On multiplying out and simplifying like terms we come up with the results:

Note that each term is a combination of a and b and the sum of the exponents are equal to 3 for each terms. The degree of each term is 3.

Thus, if we expand the question is, what are the coefficients? These coefficients are called binomial coefficients. In the expansion of the binomial coefficients are 1   3   3   1. Note that there is a "left to right" and "right to left" symmetry to the numbers. Theses coefficients can be obtained by the use of Pascal's Triangle.

Pascal's Triangle

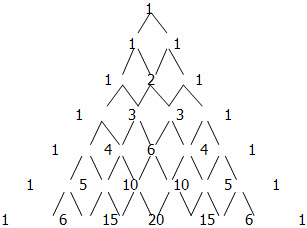
This triangular array is called Pascal's Triangle. Each row gives the combinatorial numbers, which are the binomial coefficients. That is, the row 1   2   1 are the combinatorial numbers ²C_r, which are the coefficients of (a + b)². The next row, 1   3   3   1, are the coefficients of (a + b)³; and so on.

To construct the triangle, write 1, and below it write 1   1. Begin and end each successive row with 1. To construct the intervening numbers, add the two numbers immediately above.

To construct the next row, begin it with 1, and add the two numbers immediately above: 1 + 2. Write 3. Again, add the two numbers immediately above: 2 + 1 = 3. Finish the row with 1.

There are instances that the expansion of the binomial is so large that the Pascal's Triangle is not advisable to be used. An easier way to expand a binomial raised to a certain power is through the binomial theorem. It is finding the solution to the problem of the binomial coefficients without actually multiplying out. The theorem is given as:

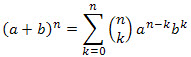
Which can be expanded as:

Remember that

is another way of writing combination

Binomial Theorem also applies to binomial with literal coefficients. It is given as:

How to solve different types of problems

Proving an expression when terms above a certain threshold can be ignored

Question

If x is too small so that terms of x³ and higher can be ignored, show that

Answer

We use the Pascal's Triangle in the expansion of (1-2x)⁶. The index of (1-2x)⁶ is 6, so we look on the 7th line of the Pascal's Triangle. The coefficients are 1, 6, 15, 20, 15, 6, 1:

Simplify the product:

Omit the term containing x³ and higher since x is too small so that terms of x³ and higher can be ignored:

Writing down an expansion of a series

Question

Write down the expansion of

.

Answer

Use the Binomial Theorem to find the expansion of

. There will be 5 terms in the expansion.

Use the expansion of

where

Evaluate the combinations and the indices:

Evaluate the product:

Finding a specific coefficient in an expansion

Question

Find the coefficient of the term x⁴ of the expansion (7x – 3)⁵:

Answer

Use the Binomial Theorem to find the term that will give x⁴ in the expansion of (7x – 3)⁵. We only want to find the coefficient of the term in x⁴ so we don't need the complete expansion.

Let a = 7x     b = –3     n = 5     n – k = 4 (since the index of x in the 1st term is 1):

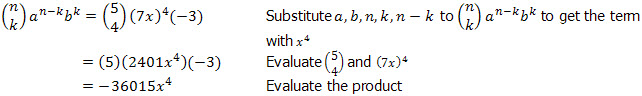
Therefore, the coefficient of the term in x⁴ in the expansion is –36015.

Go to the next page to start putting what you have learnt into practice.